全球的数据科学家们可以从任何大数据中挖掘有用的信息,从而建立模型,以便分析过去及预测未来。经过不断的潜心研究,自己终于在数据科学和机器学习方面稍微的追上了世界的脚步。我们就拿世界数据科学竞赛上比较火的泰坦尼克号乘客数据来进行数据分析及可视化,一点一点揭开数据的内在奥秘。
泰坦尼克号是由英国建造的巨型邮轮,1912年4月10日从英国英格兰南部港口城市南安普顿出发,先穿过英吉利海峡停泊在法国瑟堡,之后又停泊在了爱尔兰昆士敦,接纳了更多旅客后,它载着1324乘客和892名甲板工作人员驶向纽约,由于其船体规模相当一艘现代航空母舰,因而号称“上帝也沉没不了的巨型邮轮”,然而因为人为错误,4天后即4月14日夜泰坦尼克号撞上冰山而沉没,船上的救生艇仅能供1178人使用,但最终仅有700多人生还,1500人葬身于大西洋中,成为20世纪最大的海难事件。灾难无法挽回,但面对上述数字,人们总是好奇,究竟什么样的人可以在灾难中幸存下来,是命运使然,还是另有隐情?
特征分析
工欲善其事,我们首先引入需要的库,并读取乘客数据:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data=pd.read_csv('../input/data.csv')究竟有多少人幸存?
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
sns.countplot('Survived',data=data,ax=ax[1])
ax[1].set_title('Survived')
plt.show()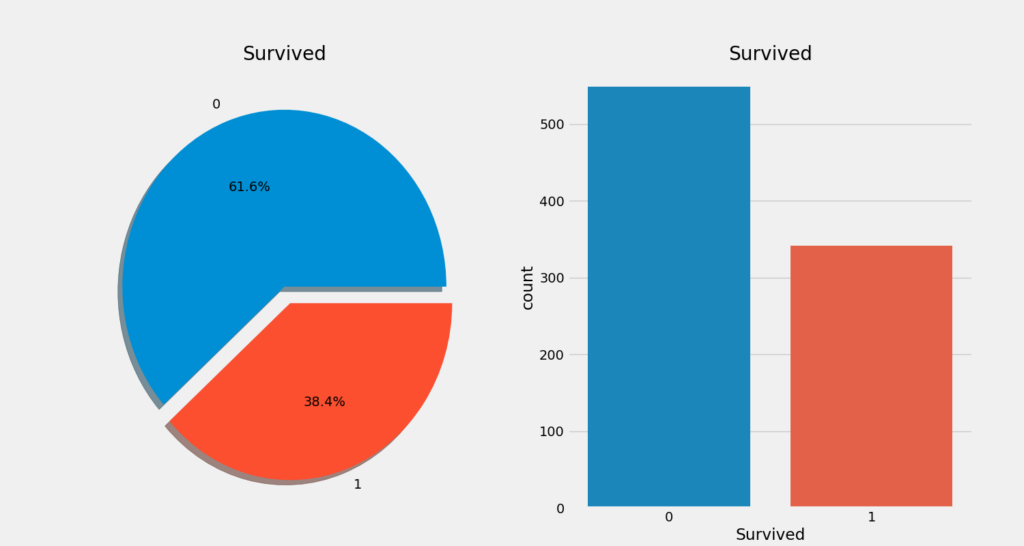
通过对数据的可视化,我们发现,幸存者数量并不多,我们需要进一步挖掘,究竟具备什么样特征的乘客能够幸存,而什么样特征的乘客会遇难。我们分别使用不同的特征,譬如性别、年龄、船舱等级以及票价等,来测试幸存率。
数据特征的类型
分类变量
分类变量是具有两个或更多类别的变量,并且该特征中的每个值可以由它们分类。例如,性别是具有两个类别(男性和女性)的分类变量。分类变量不能排序。在我们的数据中 Sex 和 Embarked 属于分类变量。
序列变量
序列变量类似于分类变量,但是它们之间的区别在于可以在这些值之间进行相对排序。例如:对于高度而言,可以有高、中、低。在我们的数据中 PClass 即船舱等级,属于序列变量。
连续变量
在坐标轴上任意两点间的数值都属于连续变量,连续变量有最大值和最小值。在我们数据中 Age 数据连续变量。
性别与幸存率
data.groupby(['Sex','Survived'])['Survived'].count()| Sex | Survived | Count |
|---|---|---|
| female | 0 | 81 |
| female | 1 | 233 |
| male | 0 | 468 |
| male | 1 | 109 |
f,ax=plt.subplots(1,2,figsize=(18,8))
data[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
sns.countplot('Sex',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Sex:Survived vs Dead')
plt.show()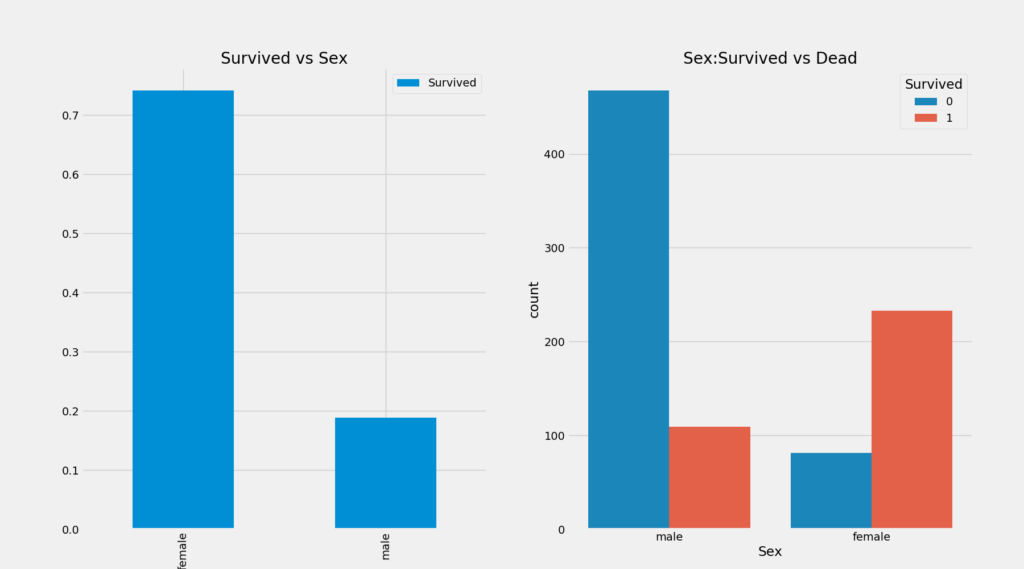
一个有趣的现象是,男性乘客数量几乎是女性乘客数量的二倍,但是男性乘客的幸存率却远低于女性乘客!
船舱等级 Pclass 与幸存率
Pclass 指船舱等级,分3个等级,1 最高,3 最低。
pd.crosstab(data.Pclass,data.Survived,margins=True).style.background_gradient(cmap='summer_r')| Survived | 0 | 1 | All |
|---|---|---|---|
| Pclass | |||
| 1 | 80 | 136 | 216 |
| 2 | 97 | 87 | 184 |
| 3 | 372 | 119 | 491 |
| All | 549 | 342 | 891 |
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Pclass'].value_counts().plot.bar(color=['#CD7F32','#FFDF00','#D3D3D3'],ax=ax[0])
ax[0].set_title('Number Of Passengers By Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Pclass:Survived vs Dead')
plt.show()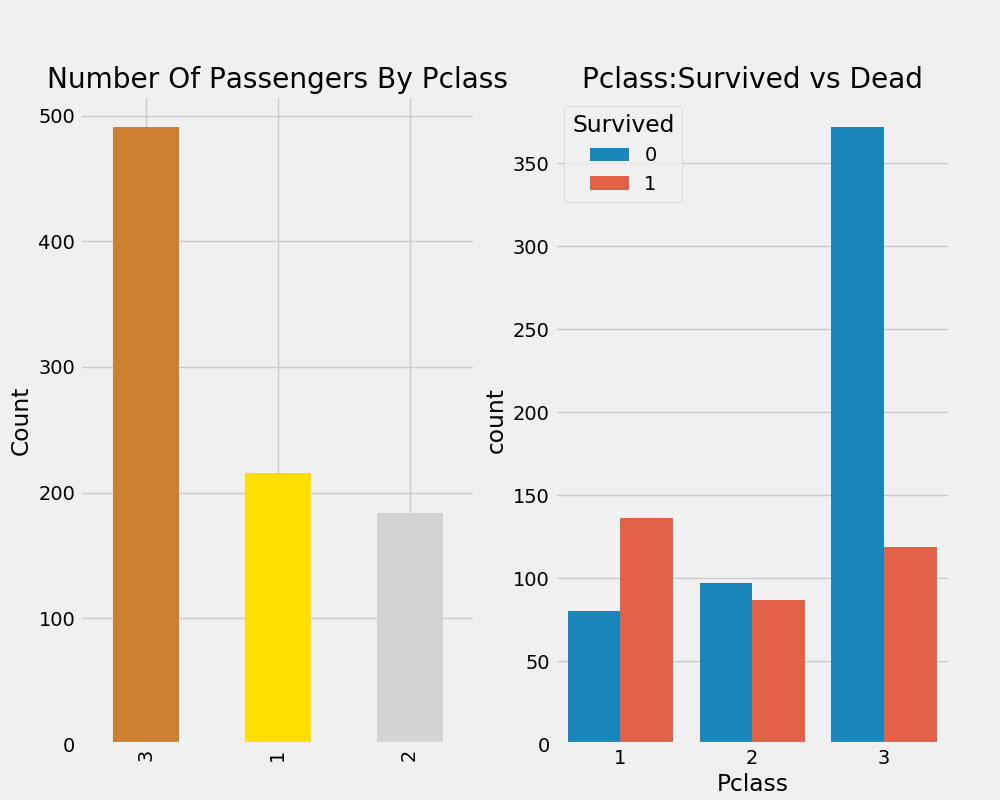
我们常说,金钱买不来所有想要的东西,但是我们通过对数据分析看出,一等舱的乘客幸存率最高,而三等舱的死亡率最高,死亡人数甚至比一等舱和二等舱死亡人数加起来的二倍还多!接下来我们把性别和船舱等级两个变量与幸存率放在一起分析:
pd.crosstab([data.Sex,data.Survived],data.Pclass,margins=True).style.background_gradient(cmap='summer_r')| Pclass | 1 | 2 | 3 | All | |
|---|---|---|---|---|---|
| Sex | Survived | ||||
| female | 0 | 3 | 6 | 72 | 81 |
| female | 1 | 91 | 70 | 72 | 233 |
| male | 0 | 77 | 91 | 300 | 468 |
| male | 1 | 45 | 17 | 47 | 109 |
| All | 216 | 184 | 491 | 891 |
sns.factorplot('Pclass','Survived',hue='Sex',data=data)
plt.show()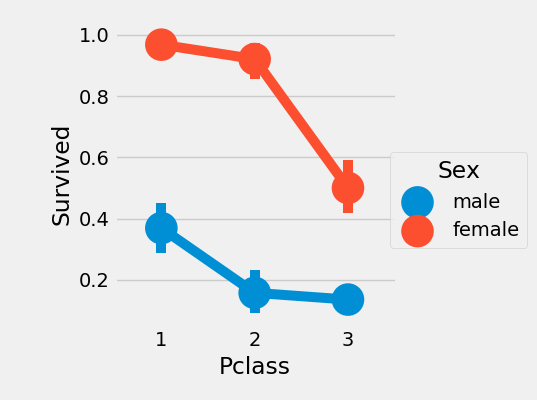
通过上述交叉表和因素图的分析我们看出,尽管船舱等级对于幸存率有影响,但是性别对于幸存率的影响更大!
年龄与幸存率
print('最老:',data['Age'].max(),'岁')
print('最年轻:',data['Age'].min(),'岁')
print('平均:',data['Age'].mean(),'岁')最老: 80.0 岁 最年轻: 0.42 岁 平均: 29.69911764705882 岁
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=data,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=data,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()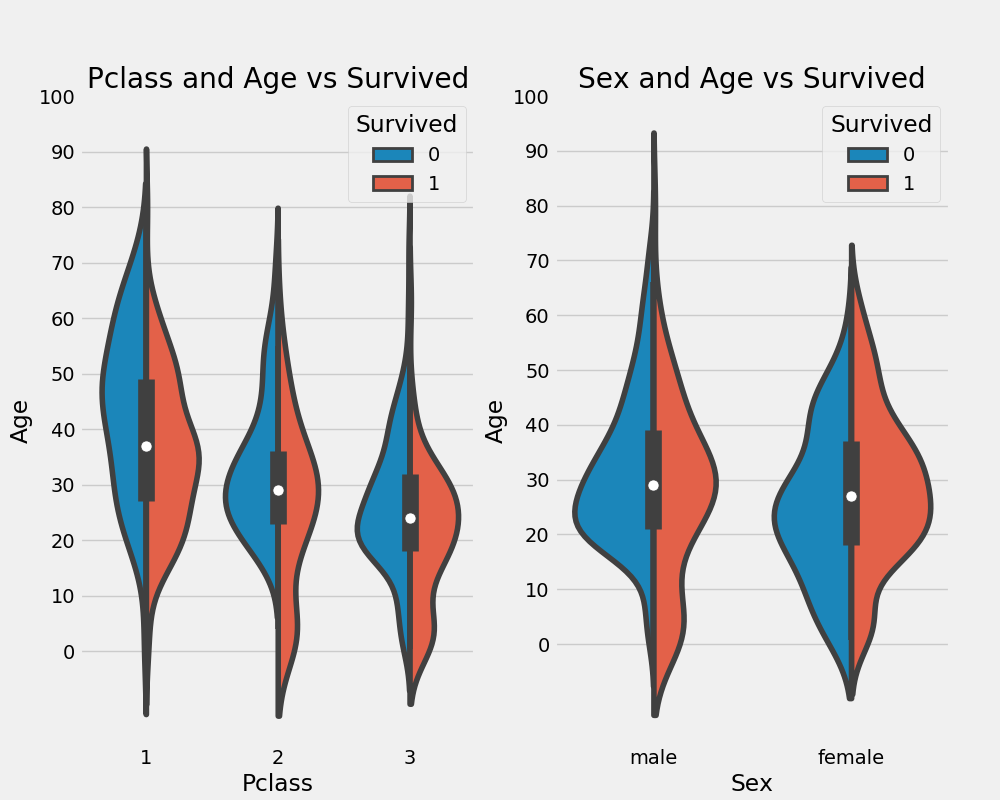
我比较喜欢的plot之一,violinplot,既可以表达幅度也可以表达密度,甚至还可以表达数据的分布,超赞!通过上图我们可以看出:
- 10岁以下儿童,船舱等级越低幸存率反而越高,貌似儿童的幸存率与船舱等级无关
- 20-50 岁的成年人,头等舱的幸存率最高
- 随着年龄增长,男性幸存率逐渐减低
票价与幸存率
print('最贵:',data['Fare'].max())
print('最便宜:',data['Fare'].min())
print('平均:',data['Fare'].mean())最贵: 512.3292 最便宜: 0.0 平均: 32.2042079685746
最低票价 $0!就是Jack的那种票吧~,看一看在不同的船舱等级中的票价分布:
f,ax=plt.subplots(1,3,figsize=(20,8))
sns.distplot(data[data['Pclass']==1].Fare,ax=ax[0])
ax[0].set_title('Fares in Pclass 1')
sns.distplot(data[data['Pclass']==2].Fare,ax=ax[1])
ax[1].set_title('Fares in Pclass 2')
sns.distplot(data[data['Pclass']==3].Fare,ax=ax[2])
ax[2].set_title('Fares in Pclass 3')
plt.show()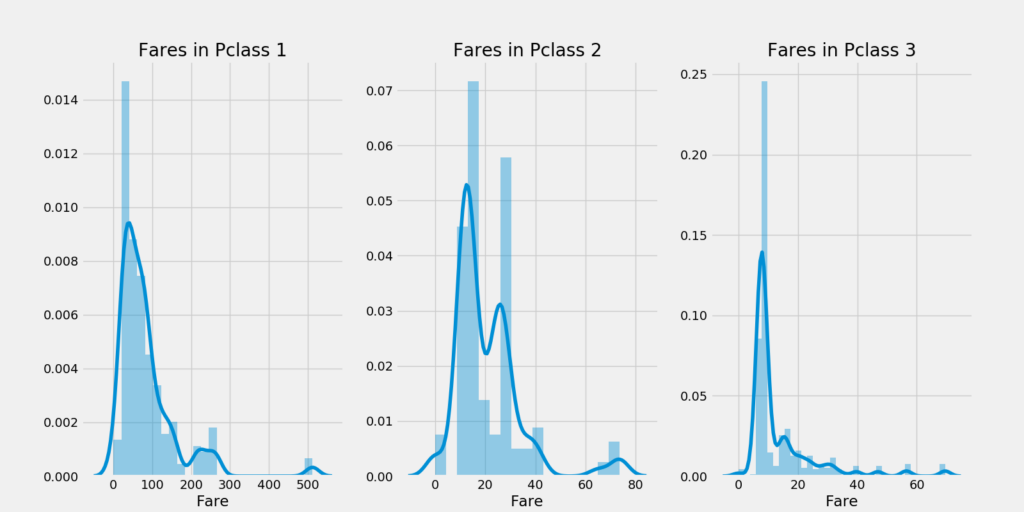
有无亲属与幸存率
乘客有无配偶及兄弟姐妹在数据中是有所体现的,那究竟这个特征对幸存率有无影响呢?
pd.crosstab([data.SibSp],data.Survived).style.background_gradient(cmap='summer_r')| Survived | 0 | 1 |
|---|---|---|
| SibSp Count | ||
| 0 | 398 | 210 |
| 1 | 97 | 112 |
| 2 | 15 | 13 |
| 3 | 12 | 4 |
| 4 | 15 | 3 |
| 5 | 5 | 0 |
| 8 | 7 | 0 |
f,ax=plt.subplots(1,2,figsize=(20,8))
sns.barplot('SibSp','Survived',data=data,ax=ax[0])
ax[0].set_title('SibSp vs Survived')
sns.factorplot('SibSp','Survived',data=data,ax=ax[1])
ax[1].set_title('SibSp vs Survived')
plt.close(2)
plt.show()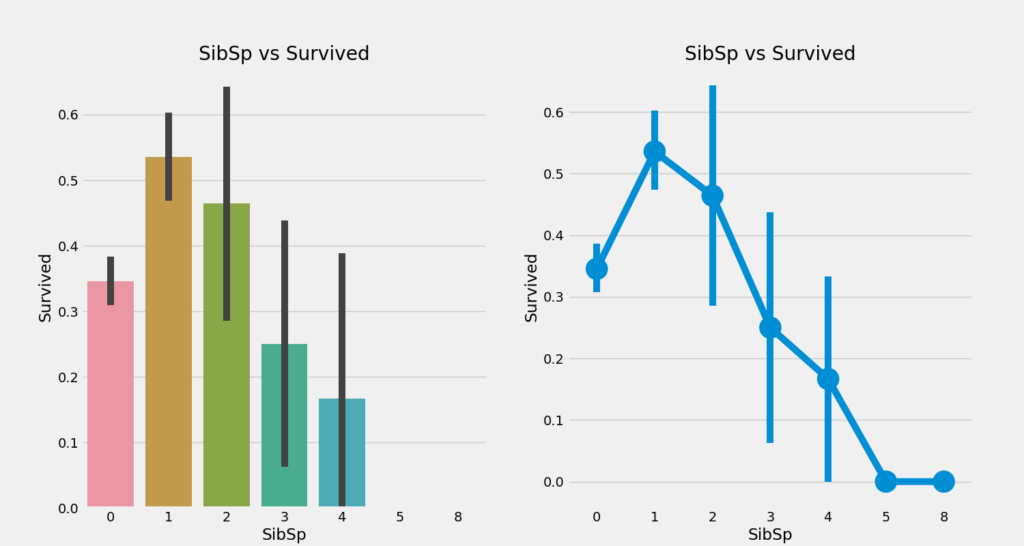
我们发现,随着亲属数量的增加,幸存率在减低,而有5-8个亲属的乘客无一幸存!
相关及预测分析
相关分析
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2) #data.corr()-->correlation matrix
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()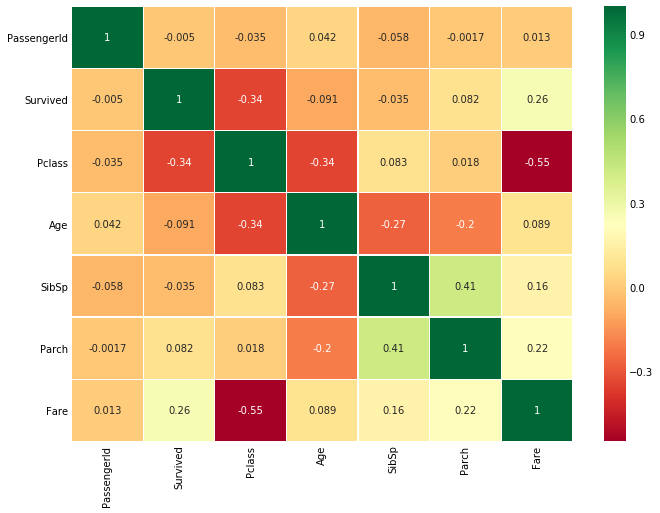
以矩阵的形式显示各变量间的相关性,图中的正负相关就不过多解释了,数据可视化后一目了然。
预测
一切数据分析的最终目的都是建立一个模型对新数据进行预测,懂得机器学习的小伙伴们都应该清楚,最简单的预测模型就是线性回归,用于解决二分类问题,但是面对大量变量、数据特征多的情况下,线性回归都难以解决实际问题。这时,逻辑回归、支持向量机、K最近邻、决策树、朴素贝叶斯及随机森林等算法就派上了用场,而且鼎鼎大名的 sklearn 都已经为我们封装好了!
from sklearn.linear_model import LogisticRegression #logistic regression
from sklearn import svm #support vector Machine
from sklearn.ensemble import RandomForestClassifier #Random Forest
from sklearn.neighbors import KNeighborsClassifier #KNN
from sklearn.naive_bayes import GaussianNB #Naive bayes
from sklearn.tree import DecisionTreeClassifier #Decision Tree
from sklearn.model_selection import train_test_split #training and testing data split
from sklearn import metrics #accuracy measure
from sklearn.metrics import confusion_matrix #for confusion matrix
from sklearn.model_selection import KFold #for K-fold cross validation
from sklearn.model_selection import cross_val_score #score evaluation
from sklearn.model_selection import cross_val_predict #prediction
train,test=train_test_split(data,test_size=0.3,random_state=0,stratify=data['Survived'])
train_X=train[train.columns[1:]]
train_Y=train[train.columns[:1]]
test_X=test[test.columns[1:]]
test_Y=test[test.columns[:1]]
X=data[data.columns[1:]]
Y=data['Survived']
kfold = KFold(n_splits=10, random_state=22) # k=10, split the data into 10 equal parts
xyz=[]
accuracy=[]
std=[]
classifiers=['Linear Svm','Radial Svm','Logistic Regression','KNN','Decision Tree','Naive Bayes','Random Forest']
models=[svm.SVC(kernel='linear'),svm.SVC(kernel='rbf'),LogisticRegression(),KNeighborsClassifier(n_neighbors=9),DecisionTreeClassifier(),GaussianNB(),RandomForestClassifier(n_estimators=100)]
for i in models:
model = i
cv_result = cross_val_score(model,X,Y, cv = kfold,scoring = "accuracy")
cv_result=cv_result
xyz.append(cv_result.mean())
std.append(cv_result.std())
accuracy.append(cv_result)
new_models_dataframe2=pd.DataFrame({'CV Mean':xyz,'Std':std},index=classifiers)
new_models_dataframe2我们将原始数据按照7:3的比例分成训练数据和测试数据,分别使用不同算法对测试数据进行交叉验证,评估预测精确度。
| Model | CV Mean | Std |
|---|---|---|
| Linear Svm | 0.793471 | 0.047797 |
| Radial Svm | 0.828290 | 0.034427 |
| Logistic Regression | 0.805843 | 0.021861 |
| KNN | 0.813783 | 0.041210 |
| Decision Tree | 0.803620 | 0.026454 |
| Naive Bayes | 0.801386 | 0.028999 |
| Random Forest | 0.813745 | 0.035245 |
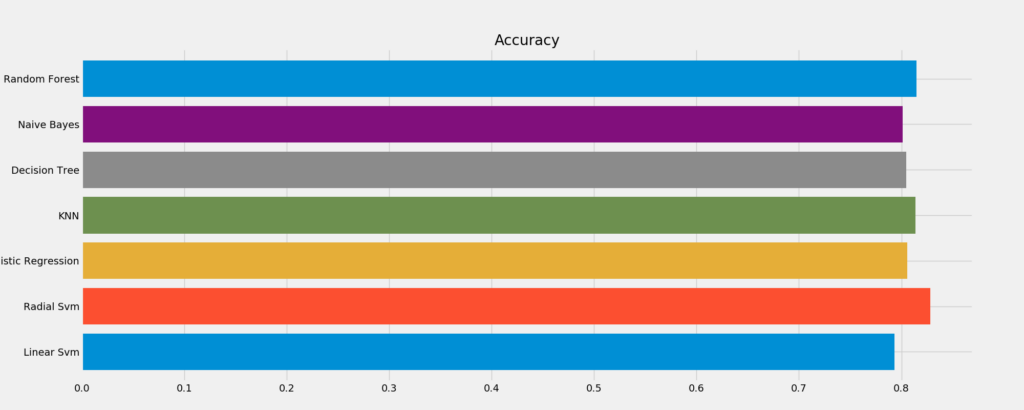
成功,模型的预测精度最高能达到 83%!下一步,争取做个神经网络模型,对新乘客预测幸存率!!
