继续计算机与医学影像的跨界之旅,本文所述内容是理解磁共振成像的K空间,并利用计算机还原和处理K空间的数据。K空间的概念在大部分书中的描述不是高深莫测就是晦涩难懂,天书之中再罗列一堆公式,医学影像小伙伴们绝对蒙!作为医学界的理工男,有责任和义务以自己的层次和认知为大家对磁共振成像中棘手的概念进行解读,尽量用最简单的语言把K空间这个事说清楚。
磁共振信号的采集和图像的重建远远复杂于CT,是至今为止最复杂的医学成像方式。我们可以通过改变射频脉冲的发射和接收时间、数据采集的方法等等,来缩短成像时间,改变图像的对比度、空间分辨率,甚至消除图像伪影。图像一旦重建完成,后续的诊断、分析和研究工作也都是以图像本身为基础进行展开,基本的物理学和医学知识是磁共振成像的基础,而脉冲序列和K空间则是磁共振成像的核心!
理解K空间之前必须要了解图像的空域、频域以及傅里叶变换的概念。
图像的空域
一幅灰度图像就是一个平面数据,而一幅彩色图像就是红绿蓝三个颜色通道叠加而成的平面数据。透过图像看这个平面数据,其实和我们看到的excel表格的内容差不多,多行多列的数据点分布在一个平面内。空域内的图像也是由许多个点组成,不同位置的点表现出不同颜色或不同灰度值,这个点叫像素,一幅我们能看得懂的图像就是许多附带位置信息的像素的数据集合,这个集合我们称之为像素域,也称空间域,简称空域。一副256阶灰度图像的灰度值从0-255分布在一定分辨率下的平面内,0为黑色,255为白色,其它灰度值在0-255数值之间离散分布。在空域对图像的处理其实就是对像素的处理,即对像素位置和大小的改变以及灰度值的改变,因此对图像进行放大、缩小、旋转、剪裁,或者由彩色变成黑白图像,再或者对黑白图像赋予伪彩等都是在图像的空域下进行。一副1920×1080分辨率的普通彩色数码图片及对应的灰度图像,以空域格式呈现出来就是我们能看懂的图像:
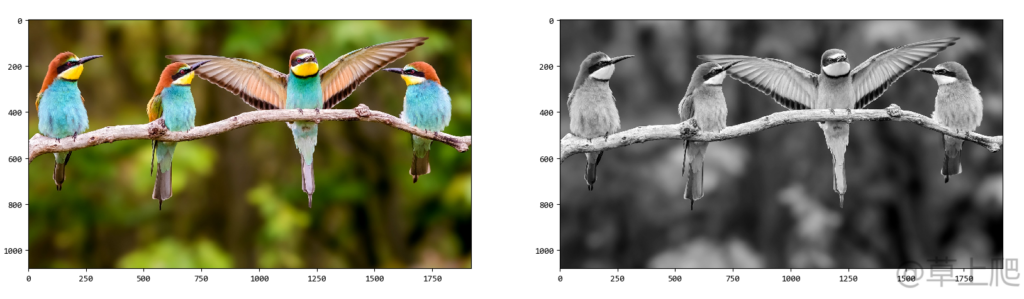
图像的频域
通过以上对空域的解释,我们可以猜到,图像的频域就是图像频率数据的集合,图像也有频率?!当然,每一个像素对应的颜色值或者灰度值,都会有个幅度,而相邻像素和像素之间幅度值的变化就反映了图像的频率差异,那么把这些频率差异按照不同位置不同振幅重新整合成一幅频谱图,就是图像的频域数据或者叫频率数据,一提到频率肯定会有振幅和相位,因此这个数据中还包含该频率对应下的振幅和相位信息。图像的频率数据分布与空域不同,空域数据的分布是按照像素值的大小组成的数据,频域则是按照频率的高低组成的数据,因此,从频域的角度理解,可以把图像分成高中低三部分频率分量。一幅图像的主要部分,其灰度值分布一般比较平坦,那么低频分量就比较强,图像的边缘及噪声的像素灰度变化非常剧烈,则为高频分量,因此,对图像进行分割、对比度增强以及降噪滤波等都应在图像的频域下进行。说到这里,医学影像界的小伙伴们可能有些蒙圈,但也是不是想到了些什么?对,几乎每一本磁共振书都会提到过的:K空间的中心部分决定磁共振图像的对比度,边缘部分决定图像细节!哎妈呀,似乎确实有些联系,先按下不表。先来看看前述同一副图像在频域下的样子:

傅里叶变换
看到这里,我们已经知道,图像其实会有两种表现形式,空域和频域,尽管两种数据格式不同,但它们反映的都是同一副图像!能对图像的两种形式进行互相变换的方法就是傅里叶变换!傅里叶变换是纯数学理论,最初应用在信号处理领域,将其应用在磁共振领域再合适不过了,由此可见学科交叉是多么重要!傅里叶变换在书本中枯燥的定义为:能将满足一定条件的某个函数表示成一系列三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。蒙圈吧,其实通俗理解,傅里叶变换有点像三棱镜的作用,白色光经过三棱镜就被分解成7色光!对于信号来讲,傅里叶变换能把混合了不同频率、不同振幅、不同相位的单一信号进行分解,同样的,经过傅里叶逆变换,也可以将七色光重建成白色光。
傅里叶变换的数学基础
磁共振接收线圈每次接收到的信号都是经激发的那个层面中的每一个氢质子所发出的信号叠加而成,而信号其实就是圆周运动在时域下的投影,且具有特定频率、振幅以及相位的正弦波,任意一个正弦波都可以由若干个简单的正弦波叠加而成,例如:
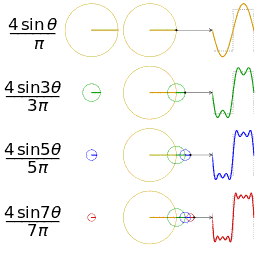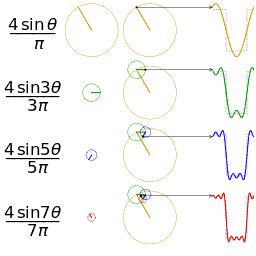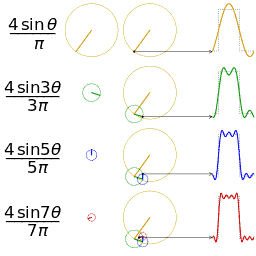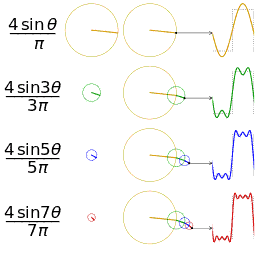
傅里叶变换的作用就是要将某个波形的信号进行分解,找到该原始信号究竟是经由哪些正弦波分量叠加而成(余弦波可由正弦波平移得到)。更复杂和深层次的数学解释请自行谷歌,咱们医学小伙伴们不必过分深究,看个图最直接:
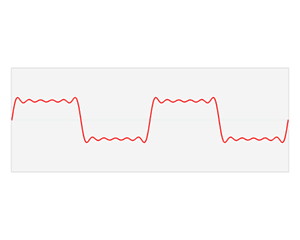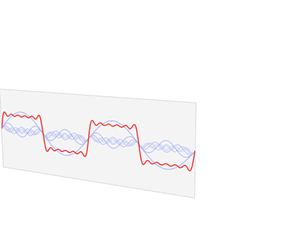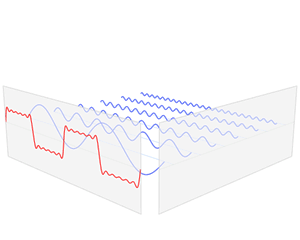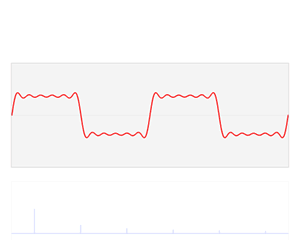
由上图可延伸出如下信号叠加的三角函数公式:
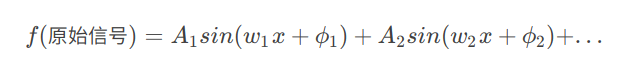
w1,w2,… 是频率的变化,A1,A2,…就是对应频率下的振幅,ϕ1,ϕ2,…就是对应频率下的相位。那么在数学上如何用一个数描述信号的振幅和相位呢?这就需要借助复数及欧拉公式,一个复数有是实部和虚部,经过运算就可以表示振幅和相位(在复平面内,实部就是圆周运动到的某个点在实数轴的投影,虚部就是在虚数轴的投影,实部和虚部的夹角就是相位,因此振幅就是实部与虚部的平方和再开方,相位就是atan(实部/虚部),即反正切三角函数,得到相位的弧度角)。欧拉公式被数学界称为”数学中最非凡的公式“,它和三角函数类似都是描述圆周运动,但它能将三角函数与复指数函数关联起来,最经典的作用就是一个实数通过欧拉公式的映射可以得到一个复数,反之便可以得到一个实数。有了振幅和相位,又能将复数映射成一个实数,我们就可以重建出一副图像,这在后边的实验中会见证。

关于傅里叶变换更详细的内容请参考如下内容:https://www.zhihu.com/question/19714540
K空间
医学影像的小伙伴们对于磁共振成像的空间编码、激发和采集的基本过程已经了解,我们应该知道磁共振K空间里的每一个点就是直接来自MR信号的数据点,那么这个数据点究竟是什么呢?磁共振的每次激发和采集前首先利用频率梯度场对人体进行选层,而选定层面内的体素则继续利用另外的频率梯度场进行频率和相位的空间编码,随后进行射频激发,我们就可以获得该层面的全层且附带空间编码的回波信号,反复以不同频率激发这个层面就会获得该层面不同频率下的回波信号,将这些回波信号们按照频率高低以及某种填充方式填入K空间中,这种数据的组织方式是不是有点像前述的图像频域数据格式?没错,K空间中的数据点其实就是最终磁共振图像的频域数据!对K空间的频域数据进行傅里叶逆变换(需要指出,杨正汉的<<磁共振成像技术指南>>K空间一节中提到的从K空间重建出磁共振图像应为傅里叶逆变换,估计是笔误,因为本文会有代码佐证。),我们就能得到频域数据对应的空域数据格式,即一副磁共振图像。这有点像前述的三棱镜,填充K空间的作用就是先准备好七色光,然后经三棱镜后我们就可得到一束白光。K空间的数据既然是频域数据,低频分量会集中在K空间的中心区域,高频分量集中在K空间的周边,因此,K空间中心部分的低频分量决定最终图像对比度,周边部分的高频分量决定图像细节。另外,在K空间中的每个数据点都包含频率的振幅和相位信息,单一数值是无法表示的,需要借助前述的复数来表达,因此K空间中数据点的数值都是复数,利用复数的实部和虚部计算出该点的的振幅和相位。这就是磁共振成像的核心,也是K空间概念的极简版,之前按下不表的地方是不是建立起了广泛联系?
还原和重建K空间数据
说了这么多,我们用计算机来加以验证。一般情况下,我们很难从磁共振主机上得到刚刚填充好的K空间原始数据,但利用傅里叶变换便可以将图像的空域数据转化成频域数据,我们仍以GE MR 750w的磁共振图像为例,将其还原出K空间数据。
之前提到过,灰度图像的空域数据中的像素点都是在0-255之间分布的灰度值,而频域数据是具有空间位置编码的信号,即利用复数形式保存的的振幅和相位信息,这就是为什么图像的频域数据会有振幅和相位两幅图。此时此刻,我们应该祭出numpy,利用它提供的快速傅里叶变换函数还原磁共振K空间数据,核心代码如下:
dicomfile_ge = pydicom.read_file('/home/ray/Downloads/ge_head_1.dcm')
img_original = dicomfile_ge.pixel_array
f = np.fft.fft2(img_original) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 移频,默认结果中心点位置是在左上角,转移到中间位置
a_fshift = np.log(np.abs(fshift)) # 取振幅
ph_fshift = np.angle(fshift) # 取相位
plt.subplot(131), plt.imshow(img_original, 'gray'), plt.title('original')
plt.subplot(132), plt.imshow(a_fshift, 'gray'), plt.title('amp')
plt.subplot(133), plt.imshow(ph_fshift, 'gray'), plt.title('phase')
plt.show()
复数形式的数据无法进行显示,因此我们提取出振幅和相位数据分别进行显示。
空域数据和频域数据尽管指向的都是同一幅图像,但其数据本质截然不同,摘要如下:

GE MR 750w 的最终图像的空域数据保存的都是16位整数形式的灰度值,而频域数据果然是复数,在我的开发环境中虚部单位用字母j表示。
有了K空间的振幅和相位数据 a_fshift 和 ph_fshift ,我们可以利用傅里叶逆变换及欧拉公式再重建出空域图像,核心代码如下:
# 逆变换--利用欧拉公式 cos(x) + isin(x) ⇔ a + ib
# 将振幅和相位整合成复数的实部和虚部,即整合成频域数据
s_real = np.exp(a_fshift)*np.cos(ph_fshift) # 整合复数的实部
s_imag = np.exp(a_fshift)*np.sin(ph_fshift) # 整合复数的虚部
s = np.zeros([512, 512], dtype=complex) # 指定数据类型为复数
s.real = np.array(s_real)
s.imag = np.array(s_imag)
fshift = np.fft.ifftshift(s) # 对整合好的频域数据进行逆变换
img_back = np.fft.ifft2(fshift)
# 出来的是复数,取绝对值,转化成实数
img_back = np.abs(img_back)
plt.subplot(141), plt.imshow(img_original, 'gray'), plt.title('original')
plt.subplot(142), plt.imshow(a_fshift, 'gray'), plt.title('amp')
plt.subplot(143), plt.imshow(ph_fshift, 'gray'), plt.title('phase')
plt.subplot(144), plt.imshow(img_back, 'gray'), plt.title('inverse fourier')
plt.show()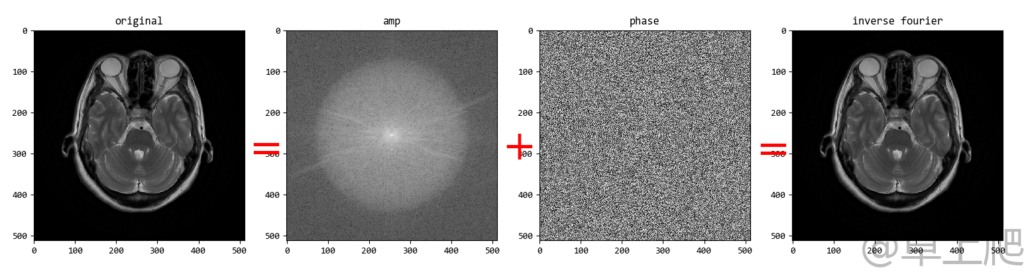
对K空间数据进行简单处理
想必每位医学影像小伙伴们都读过不少磁共振书,其中都会提到K空间中心决定图像对比度周边决定图像细节,有了以上内容做铺垫,我们就继续动手实验对K空间的数据进行简单处理来验证上述说法。我们分别创建两个滤波矩阵并与K空间的频率数据相乘,一个滤波矩阵中心部分为1(白色)周边部分为0(黑色),和K空间的数据相乘后会保留K空间中心部分的频率值,另一个滤波矩阵中心部分为0(黑色)周边部分为1(白色),和K空间的数据相乘后会保留K空间周边部分的频率值,原始K空间频域数据和滤波矩阵相乘后再经傅里叶逆变换得到的图像如下:
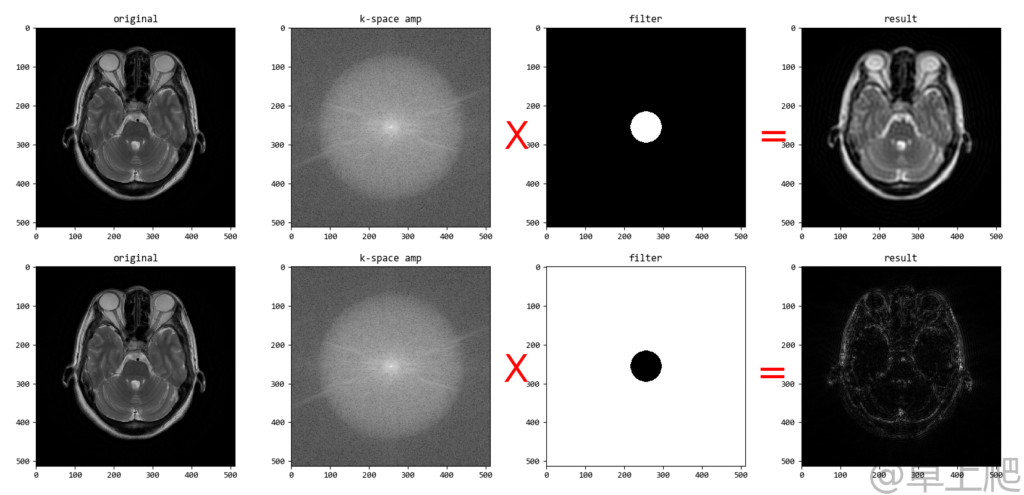
上图第一行中只利用K空间中心圆部分很少的低频分量就能重建出磁共振图像,但图像模糊、对比度稍差;上图第二行利用K空间周边部分的高频分量只能重建出图像的轮廓,而图像几乎没有对比度。由此可见K空间的中心部分对于磁共振图像重建相当重要,这也是为什么快速成像序列、扩散序列、防止运动伪影序列以及插值算法必须优先甚至反复填充K空间中心的原因。产生上图的部分核心代码如下:
def make_transform_matrix(d, image):
transform_matrix = np.zeros(image.shape)
center_point = tuple(map(lambda x: (x-1)/2, image.shape))
for i in range(transform_matrix.shape[0]):
for j in range(transform_matrix.shape[1]):
def cal_distance(pa, pb):
from math import sqrt
# d值决定中心圆大小,遍历并计算频率域中的每一个点与这个圆边界的距离
dis = sqrt((pa[0]-pb[0])**2+(pa[1]-pb[1])**2)
return dis
dis = cal_distance(center_point, (i, j))
if dis <= d:
transform_matrix[i, j] = 1
else:
transform_matrix[i, j] = 0
return transform_matrix
d_1 = make_transform_matrix(40, a_fshift) # 40 是中心园的半径
img_d1 = np.abs(np.fft.ifft2(np.fft.ifftshift(fshift*d_1)))
plt.subplot(141), plt.imshow(dicomfile_ge.pixel_array, 'gray'), plt.title('original')
plt.subplot(142), plt.imshow(a_fshift, 'gray'), plt.title('k-space amp')
plt.subplot(143), plt.imshow(d_1, 'gray'), plt.title('filter')
plt.subplot(144), plt.imshow(img_d1, 'gray'), plt.title('result')
总结
借助计算机并通过以上实验,我们知道K空间就是最终磁共振图像的频域格式,经过傅里叶逆变换将频域数据转化成空域数据格式,就是我们看得懂的图像了。有了频域数据,我们可以像处理信号一样进行滤波处理、对比度增强以及边缘分割等一系列复杂的图像处理。书本中的概念往往晦涩难懂,从那个维度去理解K空间确实让非理工科的小伙伴们不知所措,但是如果我们能摆脱专业束缚,用另一种方式去理解它,说不定就能豁然开朗、拨云见日。
